
In previous posts about modulo, we learn about the mathematician Fermat and his famous problem $$x^n + y^n = z^n.$$
Today, we will look at a geometry problem that bears his name. As we already know, Fermat was not a professional mathematician, but was a lawyer. He was doing math probably just for fun and most of his achievements that we know of today originated from his letters to his friends and also from his occasional writings on the margin of books that he read. The most famous is, of course, the problem $x^n + y^n = z^n$ and his note "I have found a beautiful proof but there is not enough space" that he wrote on the margin of the book by Diophantus.
The problem that we investigate today was raised in a letter that Fermat sent to an Italian mathematician, Torricelli. In his letter, Fermat challenged Torricelli to find a point such that the total distance from this point to the three vertices of a triangle is the minimum possible. Well, this problem was not hard for Torricelli. Since Torricelli knew how to find such a point, today some people refer to this point as the Fermat's point, and others refer it as the Torricelli's point of the triangle.
 |
| the Fermat's problem: find a point $M$ so that $MA + MB + MC$ is minimum |
To find the solution to the Fermat's problem, we are going to use a property of the ellipse. That is, if we have an ellipse with two focus points $F_1$ and $F_2$, then from any point $P$ on the ellipse if we draw a tangent line to the ellipse then this tangent line will form two equal angles with the two generator lines $PF_1$ and $PF_2$.
 |
| a property of the tangent line: $\angle xPF_1 = \angle yPF_2$ |
You can read more about this property of the tangent line to the ellipse at this post "A problem about finding shortest path and a property of the ellipse".
Going back to the Fermat problem, suppose that we have found a point $M$ so that $MA + MB + MC$ is minimum. Let us do some analysis to find out where this point should be.
Let $MA + MB = \ell$. Draw an ellipse that passes through $M$ and that has two focus points $A$ and $B$. For any point $P$ on the ellipse we have $PA + PB = MA + MB = \ell$. But because $MA + MB + MC$ is the minimum, we must have $MC \leq PC$. It means that the distance from $C$ to a point $P$ on the ellipse is minimum when $P = M$.
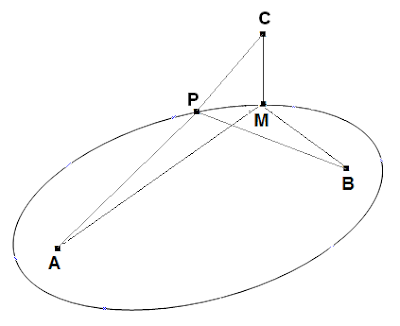 |
| from all distances from $C$ to the ellipse, $CM$ is the shortest |
Because from all distances from $C$ to the ellipse, $CM$ is the shortest, if we draw a circle with the center $C$ and radius $CM$ then this circle must touch the ellipse at one point $M$.
 |
| the circle must touch the ellipse at one point $M$ |
It follows that the ellipse and the circle must have a common tangent line that passes through $M$ as shown in the following figure.

Here we need to be a bit careful. There is an exceptional case that the ellipse and the circle may not have a common tangent line through $M$. That is when $M=A$ or $M=B$. For instance, when $M=B$ then $\ell = MA + MB = AB$, in this case there is no longer an ellipse, the ellipse has degenerated and becomes a "flat ellipse", i.e. the line segment $AB$. In the figure below, we can see that the tangent line to the circle is $cM$, on the other hand, the tangent line to the ellipse is $eM$ -- two different tangent lines.
 |
| in an exceptional case $M=B$, the tangent line to the circle is $cM$ and the tangent line to the ellipse is $eM$ |
In summary, except for the case $M=A$ or $M=B$, the circle and the ellipse will have a common tangent line through $M$ as illustrated in the figure below. By the property of the tangent line to the ellipse, we have $\angle xMA = \angle yMB$. We also have $\angle xMC = \angle yMC = 90^{o}$. Therefore, $\angle CMA = \angle CMB$.
 |
| except when $M=A$ or $M=B$, the ellipse and the circle have a common tangent line $xMy$ and $\angle CMA = \angle CMB$ |
By similar argument, we conclude that the point $M$ can only be in four positions. It is either at $A$, $B$, $C$, or a point that is specified by $\angle AMB = \angle BMC = \angle CMA$.
In the case $\angle AMB = \angle BMC = \angle CMA$ then $$\angle AMB = \angle BMC = \angle CMA = 120^{o}.$$
How interesting! The Fermat problem and the ellipse seem so unrelated, but we have used a property of the ellipse to work out possible solutions for the Fermat problem. The point $M$ so that $MA + MB + MC$ is minimum can only be in four positions. The point $M$ can be $A$, $B$, $C$, or a point such that $\angle AMB = \angle BMC = \angle CMA = 120^{o}$.
Let us stop here for now. In the next post, we will solve the Fermat problem with more details. We will see that the solution goes into two cases. The first case is when one of the angles of the triangle $ABC$ is greater than or equal to $120^{o}$. The second case is when all the angles of the triangle $ABC$ are less than $120^{o}$.
In the first case, if $\angle A \geq 120^{o}$ then the point $M$ is $A$.
In the second case, if all the angles of the triangle $ABC$ are less than $120^{o}$ then the point $M$ is the point specified by $\angle AMB = \angle BMC = \angle CMA = 120^{o}$. We can construct this point $M$ as follows. Draw outside the triangle $ABC$ three equilateral triangles $ABC'$, $BCA'$, $CAB'$. Draw three circumcircles of these equilateral triangles then these circles will meet at one common point $M$. Draw the three line segments $AA'$, $BB'$, $CC'$, then these three lines also meet at $M$ (see the figure below).
 |
| Fermat's point $M$ when $\angle A, \angle B, \angle B < 120^{o}$ |
Homework. Prove that if an ellipse and a circle tangent at one point then through this point we can draw a common tangent line for both the circle and the ellipse.

