
I would like to share with you a lesson that I have learnt. That is when facing a problem and we do not know what to do, the first thing we can do is to look at special cases of that problem. Investigating special cases can help us gain a greater understanding of the problem. To illustrate the point, let us solve some problems.
We all know that it's shorter to go straight than to go on a zigzag trail. In mathematics, it means that for any three points $A$, $B$, and $C$, the distance between $A$ and $C$ is always less than or equal to the sum of distances between $A$ to $B$ and $B$ to $C$. We call this inequality "the triangle inequality". Today, we will use this triangle inequality to solve some geometry problems.
 |
| Triangle inequality: $AC \leq AB + BC$ |
We start with the first problem. It looks obvious from the figure below that it is shorter to go from $A \rightarrow C \rightarrow B$ than to go from $A \rightarrow D \rightarrow B$ because from $AB$ the point $D$ looks further than the point $C$. The challenge is how to prove this obvious-looking fact.
 |
| it looks obvious that $AC + CB \leq AD + DB$ |
Problem 1. Given a triangle $ABD$ and a point $C$ on the triangle. Prove that $$AC +CB \leq AD + DB.$$
In mathematics, when we want to solve a problem and we don't know where to start, it is always helpful to look at some special cases first. By looking at special cases, we may understand the problem better. Sometimes, the technique that we use to solve the problem in special cases may help us to solve the problem in its general form.
In our problem, we try to put $C$ at different places and see if we can prove the inequality. First, let's say $C$ is on an edge of the triangle. Assume that $C$ is on the edge $AD$, can we prove $AC +CB \leq AD + DB$?

Well, if $C$ is on the edge $AD$, then the inequality $AC +CB \leq AD + DB$ becomes $CB \leq CD + DB$. Yes, this is the triangle inequality. So this case is solved. We quickly realize that if $C$ is on the edge $DB$ then we can prove it as well.
Going back to the problem when $C$ is a point on the triangle $ADB$, can we make $C$ on an edge of a triangle? Yes we can! By drawing the line $BC$ and make it intersect $AD$ at $E$, we can make the point $C$ lying on the edge of the triangle $AEB$. So we have $AC+CB \leq AE+EB$. But again, because $E$ is on $AD$, we have $AE+EB \leq AD +DB$. So we have solved the problem!
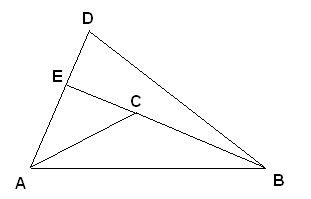
Solution to problem 1. Let $BC$ intersect with $AD$ at $E$. We have
$$AC + CB \leq AE + EC + CB = AE + EB$$
We also have
$$AE+EB \leq AE + ED + DB = AD + DB$$
Combining the two inequalities, we have $AC + CB \leq AD + DB. \blacksquare$
Let us look at the next problem.
Problem 2. Given a triangle $ABC$ and a point $M$ on $AC$. Prove that there exists a number $0 \leq \alpha \leq 1$ such that $$BM \leq \alpha BA + (1- \alpha) BC.$$

Again, let's try to prove the problem in some special cases. If $M=A$ then we need to choose $\alpha$ such that $BA \leq \alpha BA + (1- \alpha) BC$. We can see that $\alpha=1$ will satisfy.
What about $M=C$? If $M=C$ then we need to choose $\alpha$ such that $BC \leq \alpha BA + (1- \alpha) BC$. In this case $\alpha = 0$ will satisfy.
Let us now try $M$ to be the midpoint of $AC$. Will $\alpha = \frac{1}{2}$ satisfy? In other words, is it true that $BM \leq \frac{1}{2} BA + \frac{1}{2} BC$ when $M$ is the midpoint of $AC$? Can we make a triangle where one side is $BM$, another side is $\frac{1}{2} BA$ and the other side is $\frac{1}{2} BC$?

From the mid point $M$ of $AC$, if we draw a line parallel to $AB$, it will cut $BC$ at the mid point $N$. We have $MN = \frac{1}{2} AB$ and $BN = \frac{1}{2} BC$. So $BM \leq MN + BN = \frac{1}{2} AB + \frac{1}{2} BC$. We have now solved for the case $M$ is the mid point of $AC$.
We have $MN/AB= CM/CA$ so $MN = \frac{CM}{CA} AB$. We have $BN/BC = AM/AC$ so $BN = \frac{AM}{AC} BC$. But $\frac{CM}{CA} + \frac{AM}{AC} = 1$, so if we choose $\alpha = \frac{CM}{CA}$ then $1-\alpha = \frac{AM}{AC}$ and we have $BM \leq MN + BN = \alpha AB + (1-\alpha) BC$. We have solved the problem!
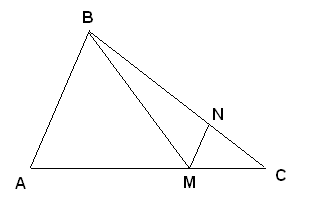
Solution to problem 2. From $M$, draw a line parallel to $AB$ and it cuts $BC$ at $N$.
We have $MN/AB= CM/CA$ so $MN = \frac{CM}{CA} AB$.
Similarly, $BN/BC = AM/AC$ so $BN = \frac{AM}{AC} BC$.
So $BM \leq MN + BN = \frac{CM}{CA} AB + \frac{AM}{AC} BC$.
If we choose $\alpha = \frac{CM}{CA}$ then $0 \leq \alpha \leq 1$ and $$BM \leq \alpha BA + (1- \alpha) BC .\blacksquare$$
That's all for now. We will look at more problems in the next post. Today we learn a lesson that when we solve a problem, it is helpful to look at special cases first. Sometimes, solving for special cases will help us to understand the problem better and may give us hint on how to tackle the problem in its general form.
Homework.

Given two triangles $ABC$ and $DBC$. Take a point $X$ on $AD$. Prove that
- The area of the triangle $XBC$ is less than or equal to the area of the triangle $ABC$ or the area of the triangle $DBC$;
- The perimeter of the triangle $XBC$ is less than or equal to the perimeter of the triangle $ABC$ or the perimeter of the triangle $DBC$.
