
To feed your curiosity, today we will look at a compass and straightedge construction of the regular polygon with 15 sides and we will show that there is a connection between this construction problem with the measuring liquid puzzle that we have learned from our previous post.
Measuring liquid puzzle

First, let us review the following brain teaser puzzle from our previous post.
Measuring liquid puzzle. Suppose you have a 3-liter jug and a 5-liter jug, how would you measure out exactly 1 liter of water?
At first glance, it seems that there are a lot of possibilities with the filling and pouring of water using the two jugs. But if we take a step back and have a careful look, we can categorize all the measuring operations into exactly 8 types:

We can see that the amount of water contained in the jugs will initially start with the value $(0,0)$, and after each step of measuring operation, this value $(a,b)$ will change into one of the following 8 possible values $$(0,b), ~~(a,0), ~~(3,b), ~~(a,5),$$ $$(0,a+b), ~~(a+b,0), ~~(a+b-5,5), ~~(3,a+b-3).$$
Therefore, we can easily prove the following fact
The amount of water (in liter) in each of the jug is always a number of the form $3 x + 5 y$ where $x$ and $y$ are two integers.
It means that if we want to measure out 1 liter of water then we have to write the value 1 in the form $3x+5y$. So our puzzle is reduced to the problem of solving the following linear Diophantine equation $$3x + 5y = 1.$$
This equation has infinitely many integer solutions. We can easily see that one solution is $(x=2,y=-1)$ and another one is $(x=-3,y=2)$. These two solutions give us the following two representations of the value 1: $${\bf 3} \times 2 - {\bf 5} \times 1 = 1$$ $${\bf 5} \times 2 - {\bf 3} \times 3 = 1.$$
Corresponding to these two representations, we have the following answers to our puzzle:
 |
| First solution ${\bf 3} \times 2 - {\bf 5} \times 1=1$: Filling 3-liter jug to the full twice and pouring out to 5-liter jug making it full once, we get 1 liter remaining. |
 |
| Second solution ${\bf 5} \times 2 - {\bf 3} \times 3=1$: Filling 5-liter jug to the full twice and pouring out to 3-liter jug making it full three times, we get 1 liter remaining. |
We have seen that our measuring liquid puzzle has a close connection with the Diophantine equation $$3x+5y=1.$$ Soon, we will see that this same Diophantine equation enables us to construct a regular polygon with 15 sides.
Regular polygon construction problem
Let us call a polygon with $n$ sides an $n$-gon. A polygon with equal sides and equal angles is called a regular polygon.
The problem of constructing regular polygons by compass and straightedge is one of a few classic problems of ancient mathematics that are easy to state but incredibly difficult to solve. For a long time, we know how to construct an equilateral triangle ($3$-gon) and a regular pentagon ($5$-gon). In his famous books, the Elements, Euclid of ancient Greek presented a method of constructing a regular pentagon. But for the next two thousand years, no one had ever succeeded in constructing a regular $7$-gon, a regular $9$-gon, a regular $11$-gon or a regular $13$-gon. It was not until in 1796, Gauss, only at age 19, made the first breakthrough by successfully constructing a regular $17$-gon. The problem was completely solved in 1837 with the following beautiful theorem
Gauss-Wantzel's Theorem. For an odd number $n$, a regular polygon of $n$ sides can be constructed by compass and straightedge if and only if $n = p_1 \times \dots \times p_t$, where $p_1$, ..., $p_t$ are distinct Fermat's primes.
Fermat's prime. A prime number is called a Fermat's prime if it has the form $$F_k = 2^{2^k}+1.$$According to this definition:
- $k=0$, $F_0 = 2^{2^0}+1 = 2^1 + 1 = 3$ is a prime, so it is a Fermat's prime,
- $k=1$, $F_1 = 2^{2^1}+1 = 2^2 + 1 = 5$ is a prime, so it is a Fermat's prime,
- $k=2$, $F_2 = 2^{2^2}+1 = 2^4 + 1 = 17$ is a prime, so it is a Fermat's prime,
- $k=3$, $F_3 = 2^{2^3}+1 = 2^8 + 1 = 257$ is a prime, so it is a Fermat's prime,
- $k=4$, $F_4 = 2^{2^4}+1 = 2^{16} + 1 = 65537$ is a prime, so it is a Fermat's prime,
- $k=5$, $F_5 = 2^{2^5}+1 = 2^{32} + 1 = 4294967297 = 641 \times 6700417$ is a composite number.
Since $3$ and $5$ are Fermat's primes, by Gauss-Wantzel's Theorem, regular $3$-gons and regular $5$-gons are constructible. In addition, since $15=3 \times 5$, regular $15$-gons are constructible. However, there is a condition in the theorem saying that the Fermat's primes have to be distinct, so $9$-gon and $25$-gon are not constructible by compass and straightedge.
Construction of a regular 15-gon
As we have seen above, $15$ is a product of two distinct Fermat's primes (3 and 5), so by Gauss-Wantzel's Theorem, a regular $15$-gon can be constructed by compass and straightedge. But how can we construct it?

Let us look at a picture of a regular $15$-gon. We can see that its vertices form a lot of equilateral triangles and a lot of regular pentagons.
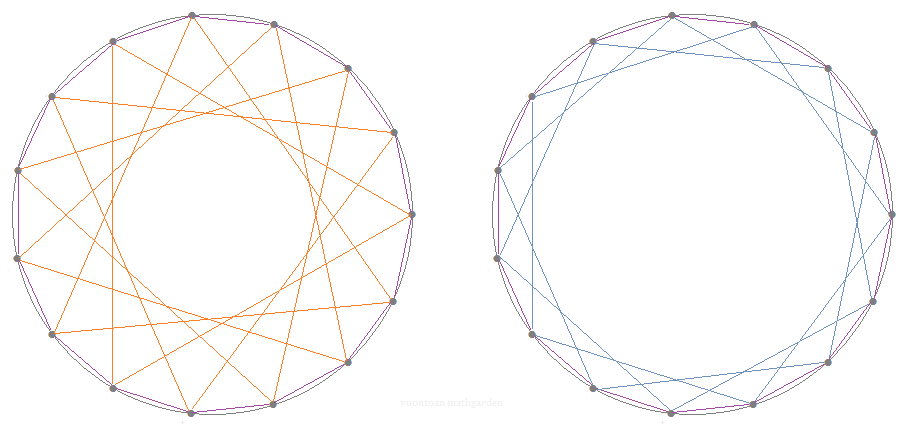
This observation motivates us to construct first an equilateral triangle and a regular pentagon. Let us draw a circle, and pick a point $P_0$ on it. We can construct an equilateral triangle $A_0 A_1 A_2$ and a regular pentagon $B_0 B_1 B_2 B_3 B_4$ with $A_0 = B_0=P_0$. Now, even though we have not constructed a regular $15$-gon fully, but at least we have a part of it!

Can we construct other vertices of the $15$-gon? YES WE CAN!!!
Looking at the above picture, we can see that we can actually construct the whole polygon because we have already had the two sides $A_1 B_2$ and $B_3 A_2$. Using compass with radius $A_1 B_2$ (or $B_3 A_2$), from $P_0$ we can construct $P_1$, from $P_1$ we can construct $P_2$, ..., and the rest of it!
Let us now write down the steps of the construction.
- Construct a circle and pick a point $P_0$ on it.
- Construct an equilateral triangle $P_0 P_5 P_{10}$ and a regular pentagon $P_0 P_3 P_6 P_9 P_{12}$.
- Connect the sides $P_5 P_6$ and $P_9 P_{10}$.
- Draw a circle with center $P_0$ and radius equal to $P_5 P_6$, this circle intersects with the original big circle at $P_1$ and $P_{14}$.
- Draw a circle with center $P_3$ and radius equal to $P_5 P_6$, this circle intersects with the original big circle at $P_2$ and $P_{4}$.
- Other vertices $P_7$, $P_8$, $P_{11}$, $P_{13}$ can be constructed similarly.

Now we know how to construct a regular $15$-gon. Let us take a step back and see why this construction is possible. The crucial part of the construction is the fact that $A_1$ and $B_2$ are next to each other, and also $B_3$ and $A_2$. This fact can be explained by the Diophantine equation $3x+5y=1$.

Indeed, if we consider the whole circle as 15 units then each side of the equilateral triangle contains 5 units and each side of the regular pentagon contains 3 units. If we use the point $P_0$ as the origin and measure the distance along the circle, then the point $A_1$ is at 5 unit, the point $A_2$ is at 10 unit. For the regular pentagon, the point $B_1$ is at 3 unit, $B_2$ 6 unit, $B_3$ 9 unit, and $B_4$ 12 unit.
In general, the point $A_i$ is at $5i$ unit and the point $B_j$ is at $3j$ unit. The distance between $A_i$ and $B_j$ along the circle is $$A_i B_j = |5i - 3j|.$$
 |
| $A_i$ is at $5i$ unit, $B_j$ is at $3j$ unit, so the distance between $A_i$ and $B_j$ is $A_i B_j = |5i - 3j|$ |
According to this distance formula, $A_i$ is next to $B_j$ if and only if the distance between $A_i$ and $B_j$ is 1 unit, that is $$5i-3j = \pm 1$$
One of the solution is $i=2$, $j=3$, this gives us $${\bf 5} \times 2 - {\bf 3} \times 3 = 1$$
this explains why $A_2$ and $B_3$ are next to each other and $B_3 A_2$ forms a side of the 15-gon.
Another solution is $i=1$, $j=2$, $${\bf 5} \times 1 - {\bf 3} \times 2 = -1$$ and this explains why $A_1$ is next to $B_2$.
So the two sides $B_3 A_2$ and $A_1 B_2$ of the regular 15-gon correspond to the two integer solutions of the Diophantine equation $3x+5y=1$. How amazing is that!
From here, we can easily have the following generalization
Draw a circle a pick a point $P_0$. Draw a regular $p$-gon $A_0 A_1 \dots A_{p-1}$ and a regular $q$-gon $B_0 B_1 \dots B_{q-1}$ with $A_0 = B_0 = P_0$. If $p$ and $q$ are two relatively prime numbers then there must exist $A_x$ and $B_y$ such that $A_x B_y$ form a side of a regular $pq$-gon. It means that if a regular $p$-gon and a regular $q$-gon are constructible then a regular $pq$-gon is also constructible.
Let us stop here for now. In our future posts, we will look at Gauss' method of constructing regular $17$-gon. Hope to see you again then.
Homework.
1. Prove the generalization mentioned at the end of the post:
Let $\gcd(p,q)=1$. If a regular $p$-gon and a regular $q$-gon are constructible by compass and straightedge then a regular $pq$-gon is also constructible.
